Bitcoin Options

I have been very busy lately trying to navigate the world burning down. I have managed to come up for air in between waves and can write a little bit about what I have been up to. There has been quite a lot of interest in regards to cryptocurrency options and it would seem like as the market has matured the options have become useful for estimating market expectations about the future distribution of prices. I studied options academically but have never traded them actively since I never fully understood how they should be used. After approaching this recently it seems pretty simple and particularly interesting in regards to crypto markets.

The Greeks

The main greeks are Delta, Gamma, Theta, Vega and Rho. I do not massively care about these from a trading point of view since the sensitivity doesn’t tell you what to do and when. Time decay (Theta) is something you can’t do much about. The main thing to know is that shorter-dated options have higher decay and that decay for ATM options follows the square root rule. Time decay gets much higher towards expiry. When choosing what expiry is the correct one when taking a position it is a question of timing, if you get the timing wrong the options will be expensive to hold.

Futures Basis (Rho) and Implied volatility (Vega) are mean-reverting.

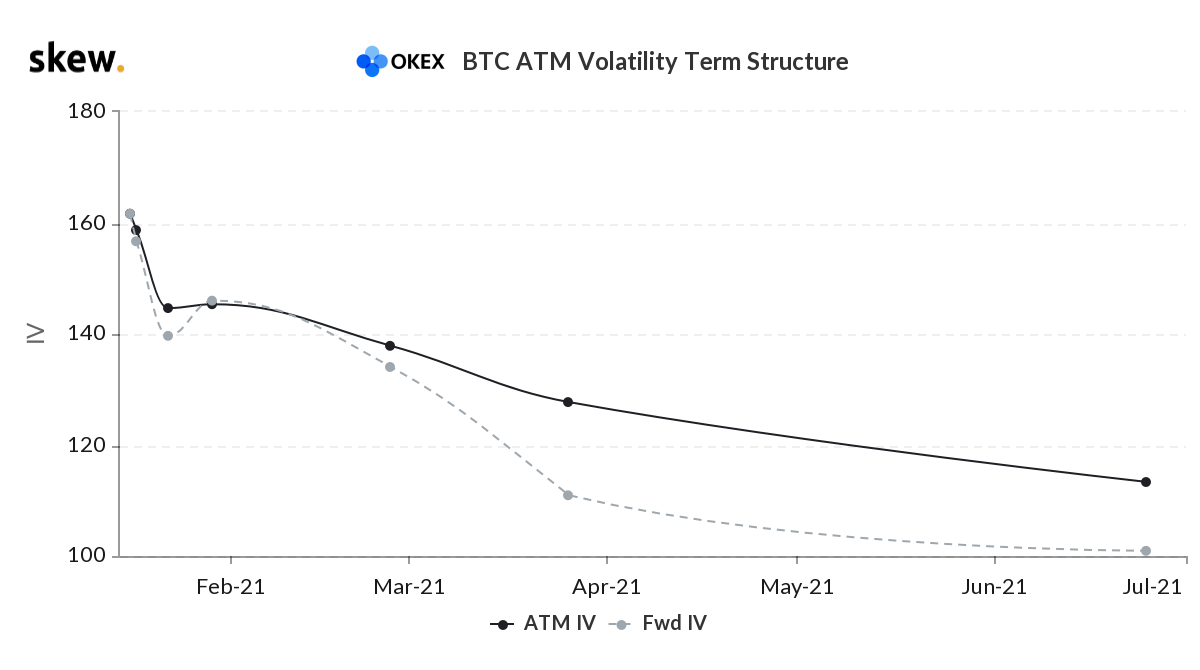
Volatility term structure 15th Jan 2021

Volatility term structure 20th Jan 2021

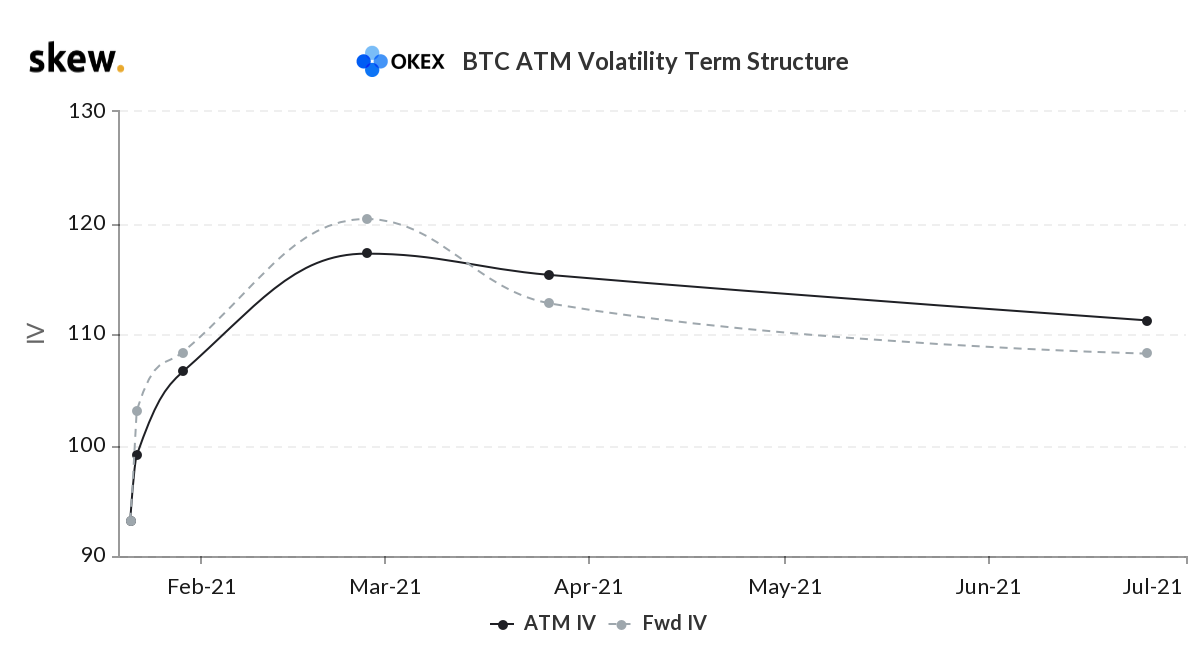
The volatility of short term options current is between 90% and 200% vol. This at least informs when options are cheap and when they are not. In regard to the future’s basis that has also been between 10% and 35%. The basis is also highly mean-reverting and can be used to work out when puts or calls are relatively cheap. High basis makes call options more expensive and put options cheaper due to the expected spot price drift over the life of the option.

Price distribution

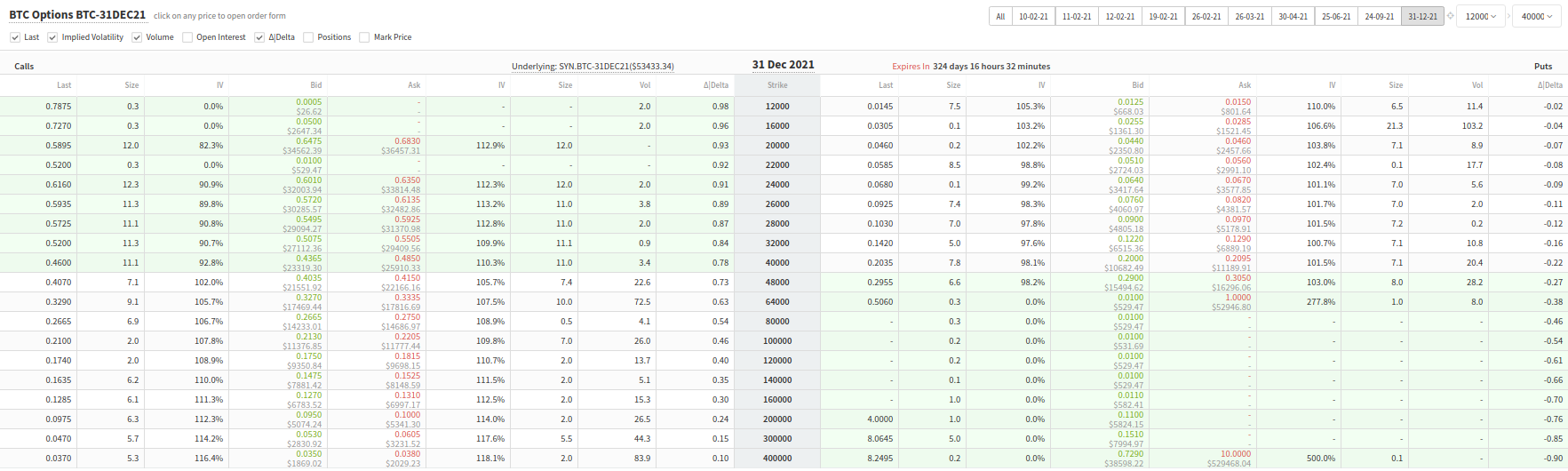
Looking at the option IV it is possible to see that there is a lot of smile. Using the formula

cdf(K, mu=future_price, std=IV * sqrt(expiry-now)/365)

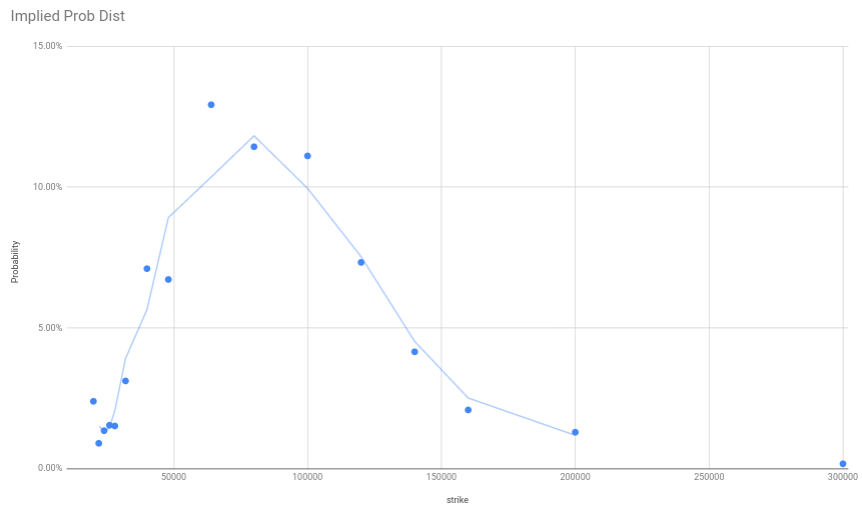
By backing out the implied cdf from the options and then differentiating it is possible to get an implied probability distribution. It is quite interesting since looking at the DEC-31-2021 options it looks like there is a large expectation that btc will be around 100k be the end of the year. The other observation I have made is that log changes don’t hold when the volatility is so high. There is effectively a positive skew purely down to the fact ln(x) ~= 1+x only for small values of x. This has been a long term artefact of bitcoin since the payoff has been so highly asymmetric.

Analytics

skew.com gives a good overview of the market and the current state of futures basis, volumes and volatility term structure.

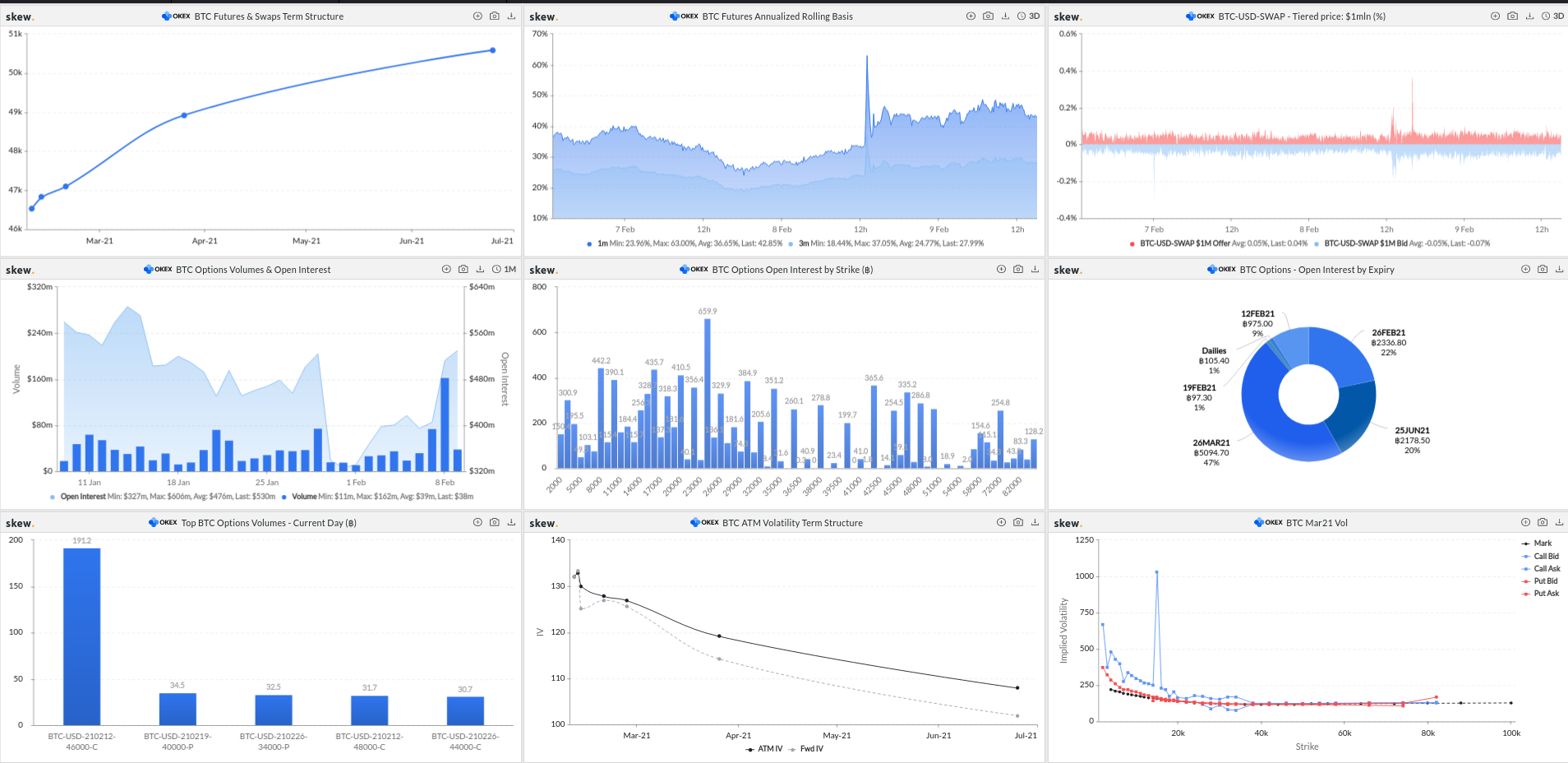
For a good dashboard then it is always useful to look at skew.com.