Fractional Differencing

To forecast prices they first need to be differenced to reduce their order of integration. The issue with integrated series is the patterns learnt from one time period dont apply to the future. If the values of the integrated series are very different, likely the learnt patterns are of little to no use. The process of calculating returns from prices is to make the series stationary to solve this issue. Stationarity is defined as

a stochastic process whose unconditional joint probability distribution does not change when shifted in time.

The main benifit of making a series stationary before fitting is that patterns learnt in the past, apply to the future.

An integrated series is defined mathematically as

In english this means that the current value is the sum of the past changes. Calculating log returns \(ln(price_t/price_{t-1)}\) or simple returns \(price_t - price_{t-1}\) however makes the assumption that prices have an order of integration of 1. The issue with the assumption is that there is information lost since the returns only contain information about the most recent two prices. In the book Advances in Financial Machine Learning the topic of fraction differencing is discussed to solve this issue. The idea is simply that the order of integration for most price series is not 0 or 1 but some value between.

Fractional Differencing

A series of fraction d is defined as

When reading about this I found it difficult to fully understand since I didn’t know what \((1-L)^d\) meant. The simplest way to think of it is a set of weights like an exponential moving average. Just like the parameter alpha \(1-\frac{1}{2^{win}}\) for an ema gives the weights of old observations, d is a single value to define all historical price weights. The value of d defines the amount of influence past prices have on the current fractionally differenced value.

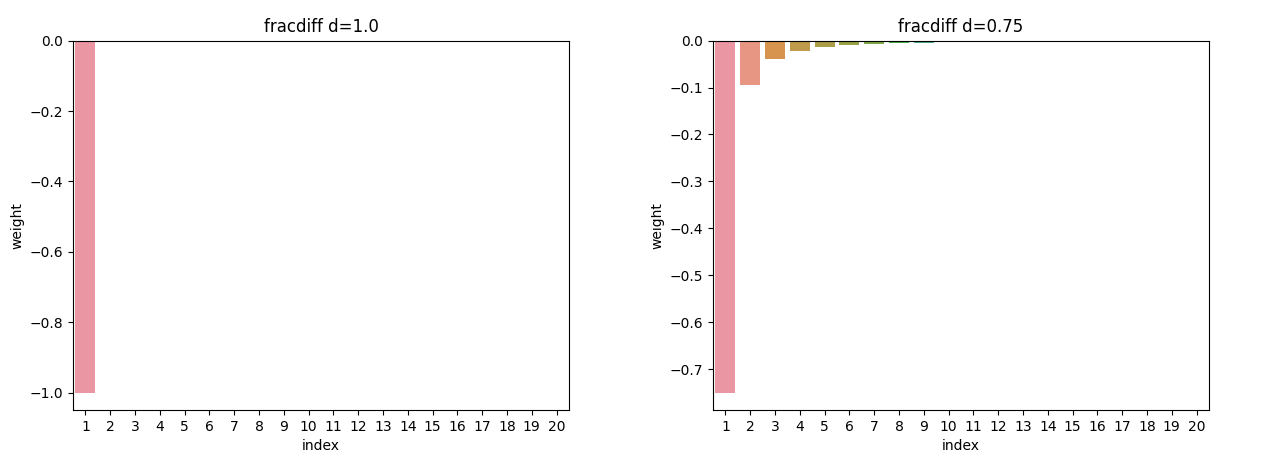
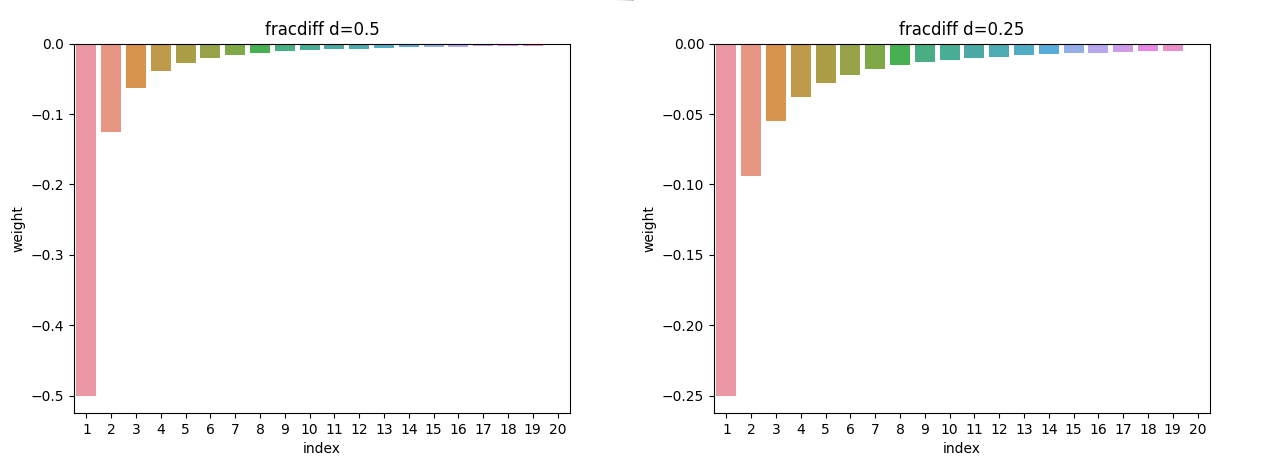
If d=1 gives the same results as standard return differencing. As d decreases the weight associated with past prices increases. The question then becomes what is the correct value of d for a given time series.

Choosing d

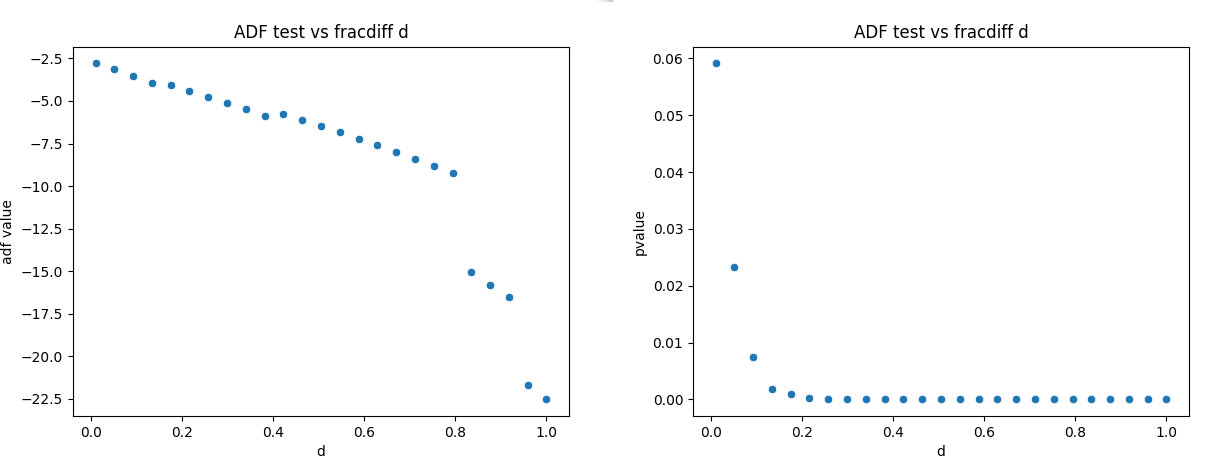
The adf test test allows the stationarity of a series to be checked. By plotting the test statistic for the ADF test for different values of fractional differencing d, we can work out the optimal value of d, to retain the largest amount of information without having problems with non-stationarity.

Code

I had issues finding an implementation of fractional differencing after reading deprado’s book. Python has a rich set of libraries but not everything is implemented. R however does have an implementation in the fracdiff library. The obvious issue is, it is written in R. One solution is to use Rpy2 in python to allow the library to be used cross-language. Looking at the implementation of diffseries in R it is simple enough to warrant porting it to python.

> library(fracdiff)
> print(diffseries)
function (x, d)
{
    x <- as.data.frame(x)
    names(x) <- "series"
    x <- x$series
    if (NCOL(x) > 1)
        stop("only implemented for univariate time series")
    if (any(is.na(x)))
        stop("NAs in x")
    n <- length(x)
    stopifnot(n >= 2)
    x <- x - mean(x)
    PI <- numeric(n)
    PI[1] <- -d
    for (k in 2:n) {
        PI[k] <- PI[k - 1] * (k - 1 - d)/k
    }
    ydiff <- x
    for (i in 2:n) {
        ydiff[i] <- x[i] + sum(PI[1:(i - 1)] * x[(i - 1):1])
    }
    ydiff
}

I wrote the following python port of the above code.

def frac_diff(x, d):
    """
    Fractionally difference time series

    :param x: numeric vector or univariate time series
    :param d: number specifying the fractional difference order.
    :return: fractionally differenced series
    """
    if np.isnan(np.sum(x)):
        return None

    n = len(x)
    if n < 2:
        return None

    x = np.subtract(x, np.mean(x))

    # calculate weights
    weights = [0] * n
    weights[0] = -d
    for k in range(2, n):
        weights[k - 1] = weights[k - 2] * (k - 1 - d) / k

    # difference series
    ydiff = list(x)

    for i in range(0, n):
        dat = x[:i]
        w = weights[:i]
        ydiff[i] = x[i] + np.dot(w, dat[::-1])

    return ydiff

This implementation can be optimised by making is fully vectorized using numpy. If you feel like writing an optimised version please feel free to share its implementation.