Savitzky Golay Filter

There are various kinds of smoothers and moving averages. One that I have used a lot and am a particular fan of is the savitsky-golay filter. The filter fits a local polynomial to the data sequentially. The main advantages of this are both that the fit is closer to the data but also the ability to fit a polynomial means that the derivatives as also easy to compute.

from scipy.signal import savgol_filter
smoothed = savgol_filter(x, window_length=127, polyorder=3, deriv=0)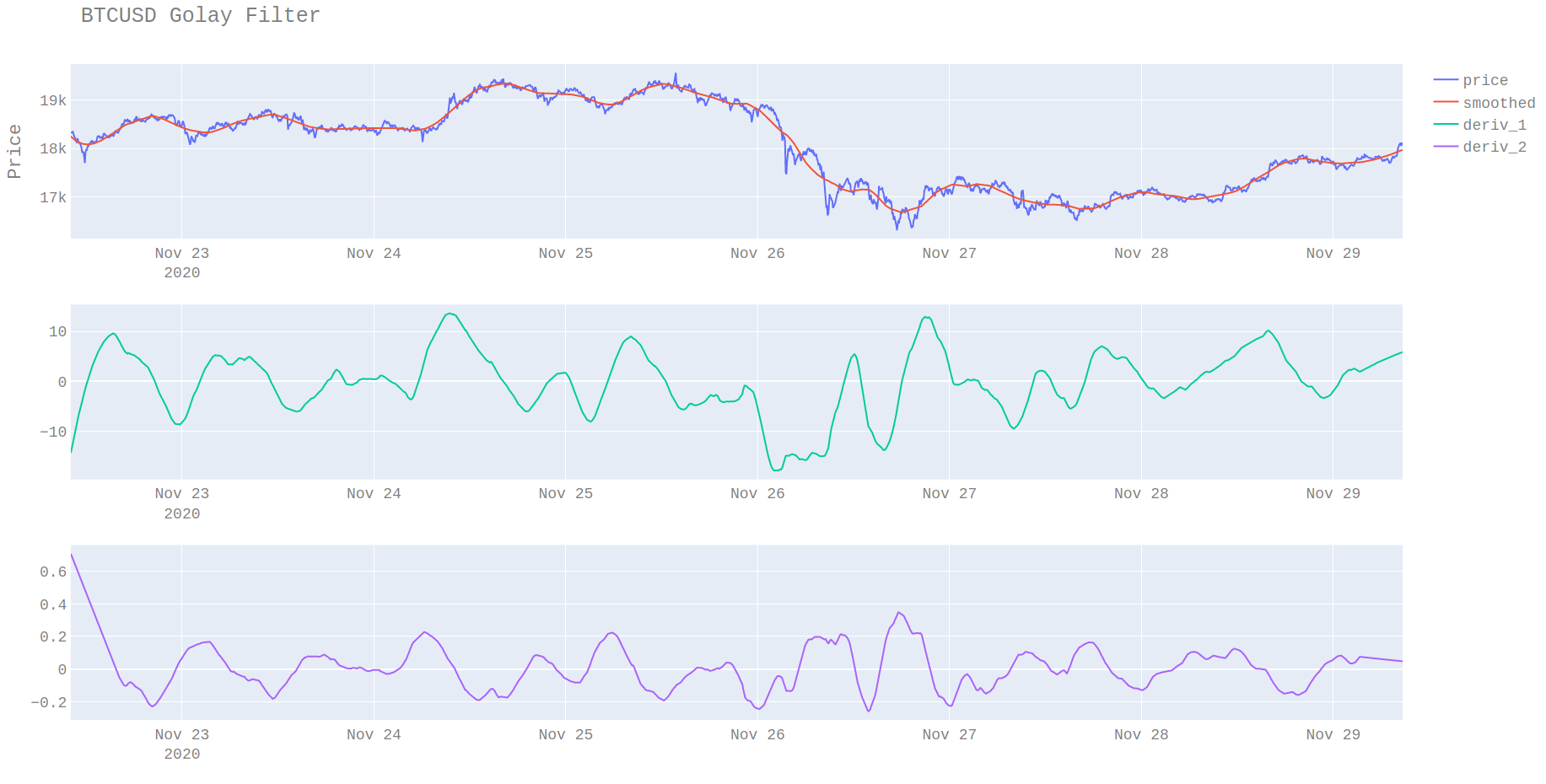

The plots show that the smoothed value is zero lag meaning it fits the data without needing to be phase-corrected (i.e. shifted).

Filter coefficients

One other good thing about the Savitsky-Golay filter is that it can be implemented as a fixed impulse response FIR either as a dot product or a convolution. The knowledge of this means that its also easy to implement mean reversion strategies between the price and the smoothed value.

from scipy.signal import savgol_coeffs
coeffs = savgol_coeffs(32, polyorder=3, deriv=0, use="dot")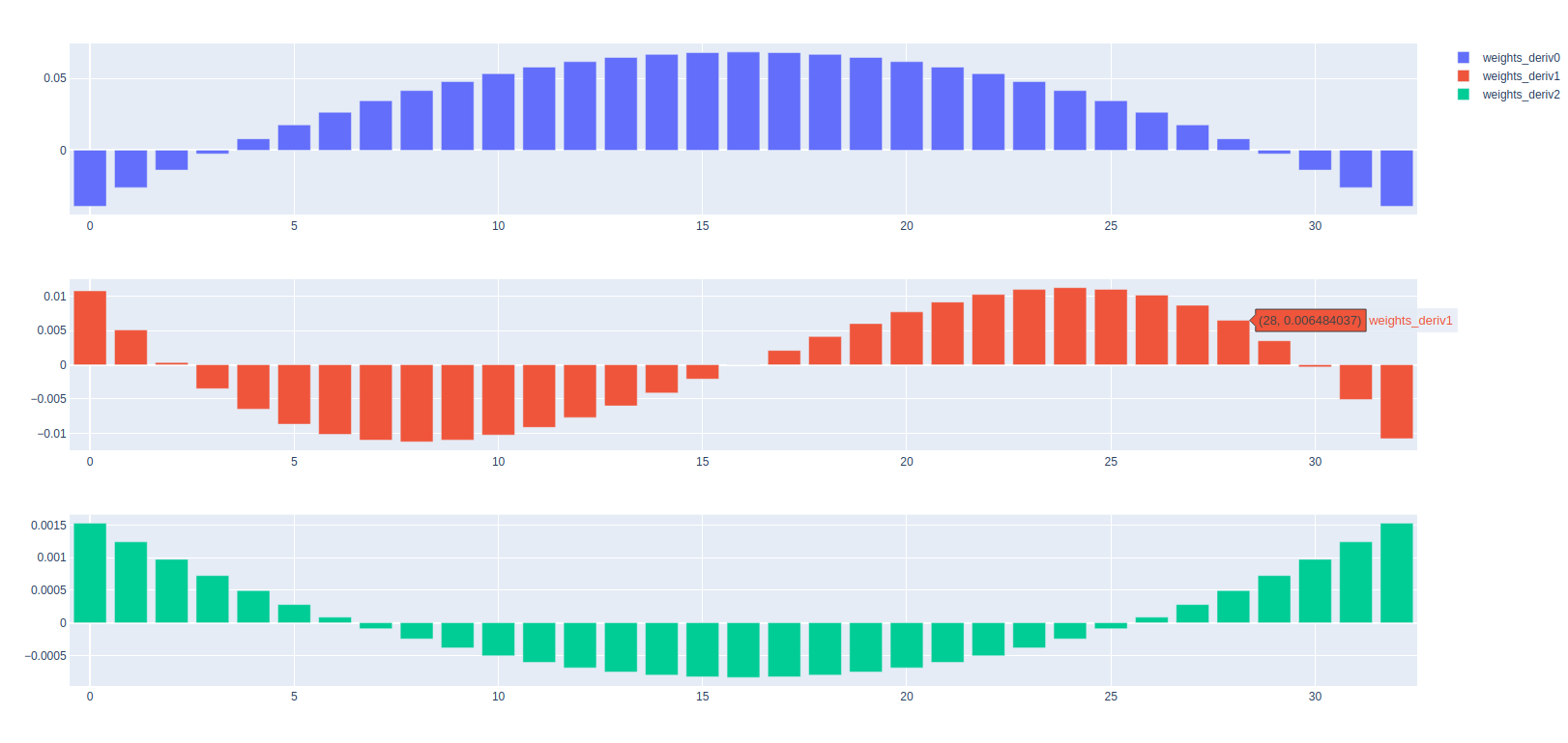

The plot of filter coefficients for different derivatives.

Issues

The main issue with Savitsky Golay filtering is one that plagues zero lag style filters. Estimates for recent observations changes as new data becomes available. In case of the scipy Golay filter implementation there are various techniques to try to estimate future data to fit the filter to. These include:

• constant
• last value
• interpolate

For any practical forecasting applications, these are all useless and give a value that overweights the most recent observation. If Golay filters are applied sequentially, and the last estimate of the filter recorded it’s easy to visualise this problem.

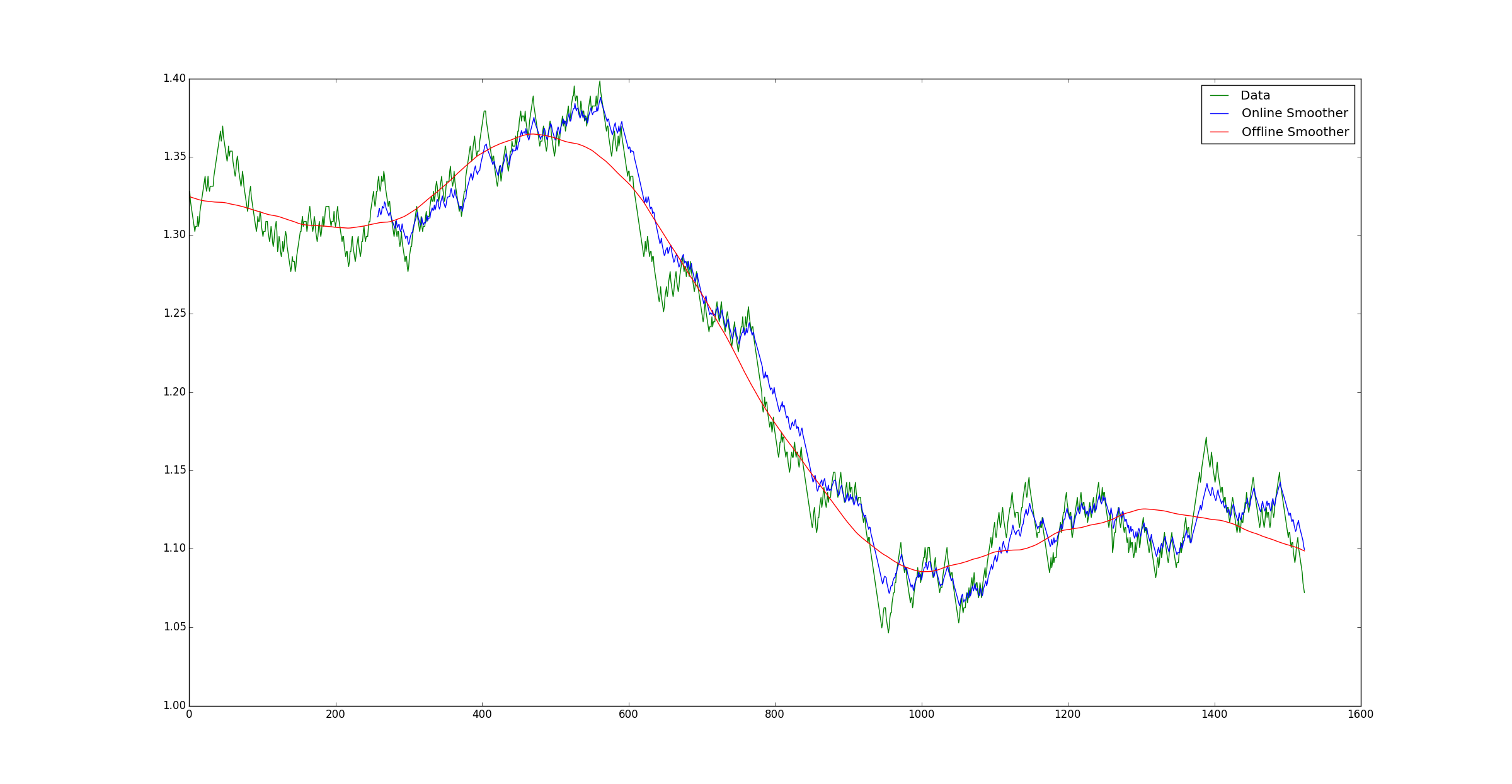
The blue line is the estimated mean at time t and the red line is the current value of the Golay filter. Without some way of estimating the future data, the filter tends to tracks the most recent prices too closely and has much higher volatility that compared with the smoothed value. If the filter did its job perfectly we would expect the blue line to exactly track the orange line that is only known at a later date.

Filter Correction

Are there better ways to estimate the missing data? Yes and that is where the derivatives are useful. If the smoothed value is thought to follow a kinematic model such as

then it is possible to forecast the moving average. I will leave this topic for a later post.